problem-抛物線運動

在抛物運動中，設初值分別為速度ν及仰角θ，試其投射之最高高度、最遠距離。已知ν= [ 10 15 20 25 ] m/s，其對應θ=[30 40 50 60]度。 1. 試撰寫一函數，並繪出其投射之軌跡。 2. 同上題，若發射點高於平面100m時，求其對應之狀況。 3. 同上題，求物體自發射後，其著地之時間。

%第一題程式碼%
close all; clear; clc disp('這是個?體運動的程式') x=input('請輸入速度\n'); y=input('請輸入仰角\n'); newton(x,y); %呼叫function%

%function newton%
function [h,r,y1]=newton(v,th);
sa=size(v);
g=9.81;
h=(v.^2.*(sind(th)).^2)./(2*g);
r=(v.^2.*sind(th.*2))./g;
for n=1:sa(1,2)
    s=linspace(0,r(n));
    y1=tand(th(n)).*s-(g./(2.*v(n).^2.*(cosd(th(n))).^2).*(s.^2));
    plot(s,y1);  
    text(r(n)/2,h(n),sprintf('最高為%2.5f',h(n)))
    text(r(n),0,sprintf('最遠處%2.3f',r(n)))
    hold on
end
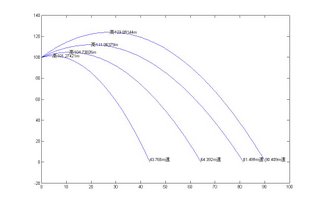
%執行結果%

%第二題和第三題程式碼%
close all;
clear;
clc
disp('這是個?體運動的程式')
x=input('請輸入速度\n');
y=input('請輸入仰角\n');
z=input('請輸入高度\n')
newton1(x,y,z); %呼叫Function newton1%
%function newton1%
function [h,r,y1]=newton1(v,th,h1);
sa=size(v);
g=9.81;
t=(v.*sind(th)+sqrt((v.*sind(th)).^2+(4.*0.5.*g.*h1)))./g
h=h1+(v.^2.*(sind(th)).^2)./(2*g);
r=v.*cosd(th).*t
for n=1:4
    s=linspace(0,r(n));
    y1=(tand(th(n)).*s-(g./(2.*v(n).^2.*(cosd(th(n))).^2).*(s.^2)))+h1;
    plot(s,y1);
    text(((v(n).^2.*sind(th(n).*2))/g)/2,h(n),sprintf('高%2.5fm',h(n)))
    text(r(n),0,sprintf('%2.3fm遠\t\t\n ',r(n)))    
    hold on
end
%執行結果%
t(著地時間) =
5.0536    5.6038    6.3395    7.2327